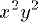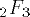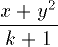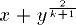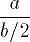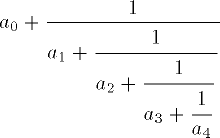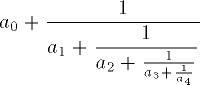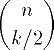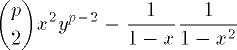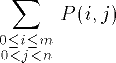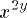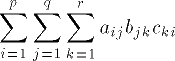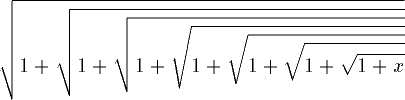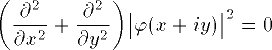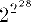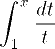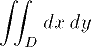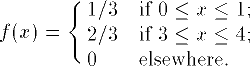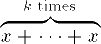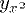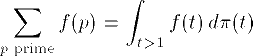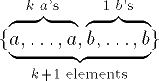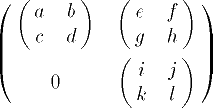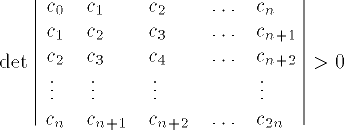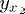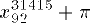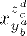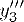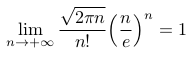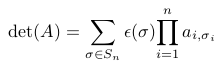Mozilla Torture Test

This page reproduces the tests from
https://www-archive.mozilla.org/projects/mathml/demo/texvsmml.xhtml and
https://fred-wang.github.io/MathFonts/mozilla_mathml_test/

Images from LaTeX are also included for comparison.

	Source	Temml	Comment
1	x^2y^2	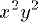$x^{2} y^{2}$	TeXbook p128
2	_2F_3	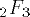$_{2} F_{3}$	TeXbook p128
3	x+y^2\over k+1	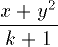$\frac{x + y^{2}}{k + 1}$	TeXbook p139
4	x+y^{2\over k+1}	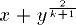$x + y^{\frac{2}{k + 1}}$	TeXbook p139
5	a\over{b/2}	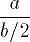$\frac{a}{b / 2}$	TeXbook p139
6	a_0 + \cfrac{1}{a_1 + \cfrac{1}{a_2 + \cfrac{1}{a_3 + \cfrac{1}{a_4}}}}	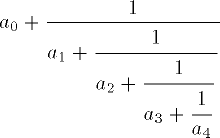$a_{0} + \frac{1}{a_{1} + \frac{1}{a_{2} + \frac{1}{a_{3} + \frac{1}{a_{4}}}}}$	TeXbook p142
7	a_0+{1\over a_1+{1\over a_2+{1\over a_3+ {1\over a_4}}}}	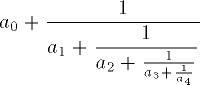$a_{0} + \frac{1}{a_{1} + \frac{1}{a_{2} + \frac{1}{a_{3} + \frac{1}{a_{4}}}}}$	TeXbook p142
8	n\choose {k / 2}	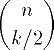$(\binom{n}{k / 2})$	TeXbook p143
9	{p \choose 2} x^2 y^{p-2} 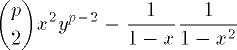{1\over{1-x}} {1\over{1-x^2}}	$(\binom{p}{2}) x^{2} y^{p - 2} - \frac{1}{1 - x} \frac{1}{1 - x^{2}}$	TeXbook p143
10	\sum_{\scriptstyle 0 \le i \le m \atop \scriptstyle 0 < j < n} P(i, j)	$\sum_{\binom{0 \leq i \leq m}{0 < j < n}} P (i, j)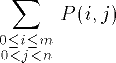$	TeXbook p145
11	x^{2y}	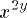$x^{2 y}$	TeXbook p128
12	\sum_{i=1}^p \sum_{j=1}^q \sum_{k=1}^r a_{ij}b_{jk}c_{ki}	$\sum_{i = 1}^{p} \sum_{j = 1}^{q} \sum_{k = 1}^{r} a_{i j} b_{j k} c_{k i}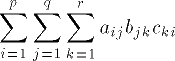$	TeXbook p145
13	\sqrt{1+\sqrt{1+\sqrt{1+ \sqrt{1+\sqrt{1+\sqrt{1+ \sqrt{1+x}}}}}}}	$\sqrt{1 + \sqrt{1 + \sqrt{1 + \sqrt{1 + \sqrt{1 + \sqrt{1 + \sqrt{1 + x}}}}}}}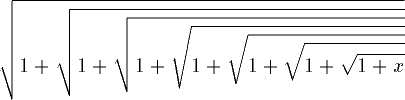$	TeXbook p145
14	\bigg(\frac{\partial^2} {\partial x^2} + \frac {\partial^2}{\partial y^2} \bigg){\big\lvert\varphi (x+iy)\big\rvert}^2	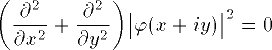$(\frac{\partial^{2}}{\partial x^{2}} + \frac{\partial^{2}}{\partial y^{2}}) {\| φ (x + i y) \|}^{2}$	TeXbook p147
15	2^{2^{2^x}}	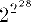$2^{2^{2^{x}}}$	TeXbook p128
16	\int_1^x {dt\over t}	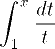$\int_{1}^{x} \frac{d t}{t}$	TeXbook p168
17	\int\!\!\!\int_D dx,dy	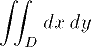$\int \int_{D} d x d y$	TeXbook p169
18	f(x) = \begin{cases}1/3 & \text{if }0 \le x \le 1; \\ 2/3 & \text{if }3\le x \le 4;\\ 0 &\text{elsewhere.} \end{cases}	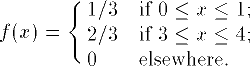$f (x) = {\begin{matrix} 1 / 3 & if 0 \leq x \leq 1; \\ 2 / 3 & if 3 \leq x \leq 4; \\ 0 & elsewhere. \end{matrix}$	TeXbook p175
19	\overbrace{x +\cdots + x} ^{k \text{ times}}	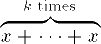$\overset{k times}{\overset{⏞}{x + \dots + x}}$	TeXbook p176
20	y_{x^2}	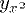$y_{x^{2}}$	TeXbook p128
21	\sum_{p\text{ prime}} f(p)=\int_{t>1} f(t)d\pi(t)	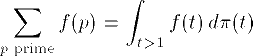$\sum_{p prime} f (p) = \int_{t > 1} f (t) d π (t)$	TeXbook p181
22	{\underbrace{\overbrace{ \mathstrut a,\dots,a}^{k ,a\rq\text{s}},\overbrace{ \mathstrut b,\dots,b}^{l, b\rq\text{s}}}_{k+l \text{ elements}}}	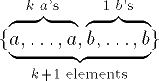${\underset{k + l elements}{\underset{⏟}{\overset{k a^{'} s}{\overset{⏞}{a, \dots, a}}, \overset{l b^{'} s}{\overset{⏞}{b, \dots, b}}}}}$	TeXbook p181
23	\begin{pmatrix} \begin{pmatrix}a&b\\c&d \end{pmatrix} & \begin{pmatrix}e&f\\g&h \end{pmatrix} \\ 0 & \begin{pmatrix}i&j\\k&l \end{pmatrix} \end{pmatrix}	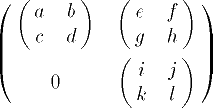$(\begin{array}{cc} (\begin{array}{cc} a & b \\ c & d \end{array}) & (\begin{array}{cc} e & f \\ g & h \end{array}) \\ 0 & (\begin{array}{cc} i & j \\ k & l \end{array}) \end{array})$	TeXbook p181
24	`\det\begin{vmatrix}` `c_0&c_1&c_2&\dots& c_n\\` `c_1 & c_2 & c_3 & \dots &` `c_{n+1}\\ c_2 & c_3 & c_4` `&\dots & c_{n+2}\\ \vdots` `&\vdots&\vdots & &\vdots` `\\c_n & c_{n+1} & c_{n+2}` `&\dots&c_{2n}` `\end{vmatrix} > 0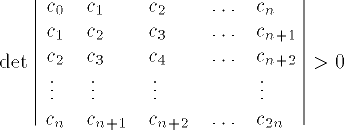`	$\det \| \begin{array}{ccccc} c_{0} & c_{1} & c_{2} & \dots & c_{n} \\ c_{1} & c_{2} & c_{3} & \dots & c_{n + 1} \\ c_{2} & c_{3} & c_{4} & \dots & c_{n + 2} \\ ⋮ & ⋮ & ⋮ & ⋮ \\ c_{n} & c_{n + 1} & c_{n + 2} & \dots & c_{2 n} \end{array} \| > 0$	TeXbook p181
25	y_{x_2}	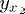$y_{x_{2}}$	TeXbook p128
26	x_{92}^{31415} + \pi	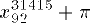$x_{92}^{31415} + π$	TeXbook p129
27	x_{y^a_b}^{z^c_d}	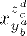$x_{y_{b}^{a}}^{z_{d}^{c}}$	TeXbook p129
28	y_3'''	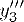$y_{3}^{'''}$	TeXbook p130
29	\lim_{n\rightarrow+\infty} {\sqrt{2\pi n}\over n!} \genfrac (){}{}n{e}^n = 1	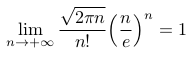$\lim_{n \to + \infty} \frac{\sqrt{2 π n}}{n!} {(\frac{n}{e})}^{n} = 1$
30	\det(A) = \sum_{\sigma \in S_n} \epsilon(\sigma) \prod_{i=1}^n a_{i, \sigma_i}	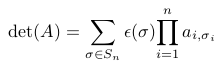$\det (A) = \sum_{σ \in S_{n}} ϵ (σ) \prod_{i = 1}^{n} a_{i, σ_{i}}$